高品质因子共振型介质超构表面中的模式耦合行为的研究

作者: irglass 时间: 2022-12-10 浏览:979 次

近期，我室高一骁博士、沈祥研究员等联合英国诺丁汉特伦特大学研究团队在共振型介质超构表面的研究工作中取得进展，并在Optics Express上发表题为“Q-factor mediated quasi-BIC resonances coupling in asymmetric dimer lattices”的论文[1]。

高品质因子共振型介质超构表面在非线性光学、纳米激光、传感等领域具有重要的应用前景。“连续域中的束缚态（Bound states in the continuum，BIC）”这一概念提供了一种通过单元结构对称性来灵活操控超构表面共振品质因子的新方法。前期高一骁等（见文献[2]）发现了在二聚体单元结构（如图1a所示）中存在两种对称性保护的BIC共振，即平移对称性和反射对称性保护的BIC共振，如图1c所示，而且通过对单元结构不同对称性的微扰，两类BIC共振的Q因子可以独立调节，如图1d-e所示。

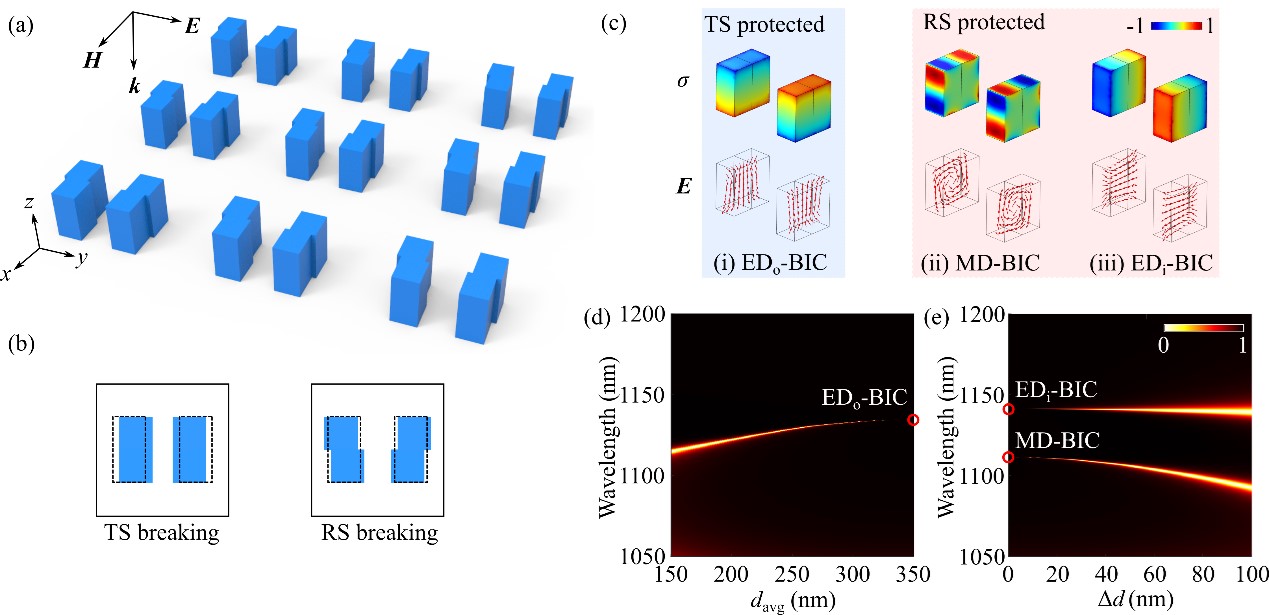
图1 （a）基于介质纳米块二聚体结构的非对称超构表面示意图。（b）对二聚体单元结构的平移对称性（Translational symmetry，TS）和反射对称性（Reflection symmetry，RS）的扰动示意图。（c）TS保护的EDo-BIC和RS保护的EDi-BIC和MD-BIC模式的表面电荷和电场分布图。（d）对单元结构仅进行TS扰动的透射谱，（e）对单元结构仅进行RS扰动的透射谱。

共振模式的耦合效应可以灵活调控光谱特性。在Optics Express的工作中，作者聚焦在三种BIC模式，即受到平移对称性（TS）保护的面外偶极BIC模式（EDo-BIC），和受到反射对称性（RS）保护的面内电偶极子BIC模式（EDi-BIC）和磁偶极子BIC模式（MD-BIC）。通过调控单元结构的几何参数，可以使这三种BIC共振模式的共振波长发生交叉，从而触发模间耦合，如图2a所示。如果在单元结构中引入TS和RS的扰动，在平面波激励下，则在透射谱中表现为相互正交的EDi-BIC和EDo-BIC会直接交叉，如图2b中黄圈所示，而非正交的MD-BIC和EDo-BIC展现出反交叉的特征，如图2b中白圈所示。

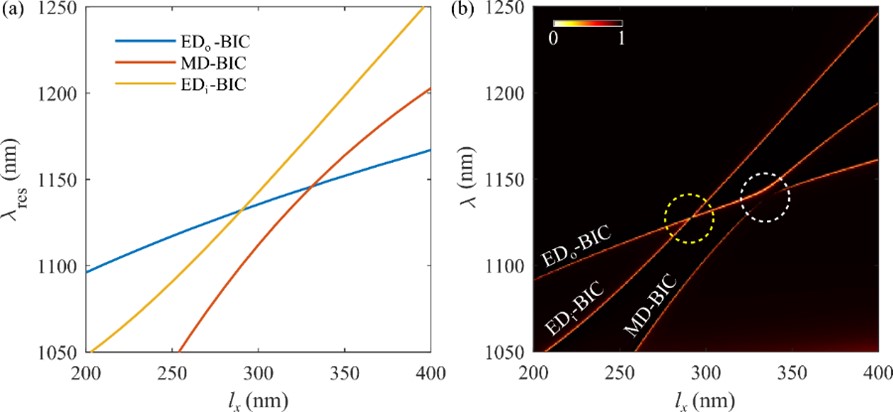
图2（a）三类不同的BIC共振模式的波长随着二聚体长度变化。（b）在引入RS和TS微扰之后，共振超构表面的透射光谱随着二聚体长度的演变。

作者围绕这两种不同的BIC耦合行为，进一步探索了Q因子对耦合行为的调控规律。

首先，作者研究了两个正交的BIC模式的耦合行为，在几种不同程度的RS扰动下，EDi-QBIC模式和EDo-QBIC模式的Q值相对大小会发生变化，在共振交叉处，透射谱的行为会发生显著的变化，如图3所示。在交叉之处，两个模式的干涉现象会引起减小共振带来的反射，合理调控两者的品质因数，会出现一种纯相位调控的情况，这一现象被称为极限惠更斯超构表面，在相位调制中有潜在的应用前景。如果增大两个Q因子的差值，共振交叉之处会出现电磁诱导透明的现象。

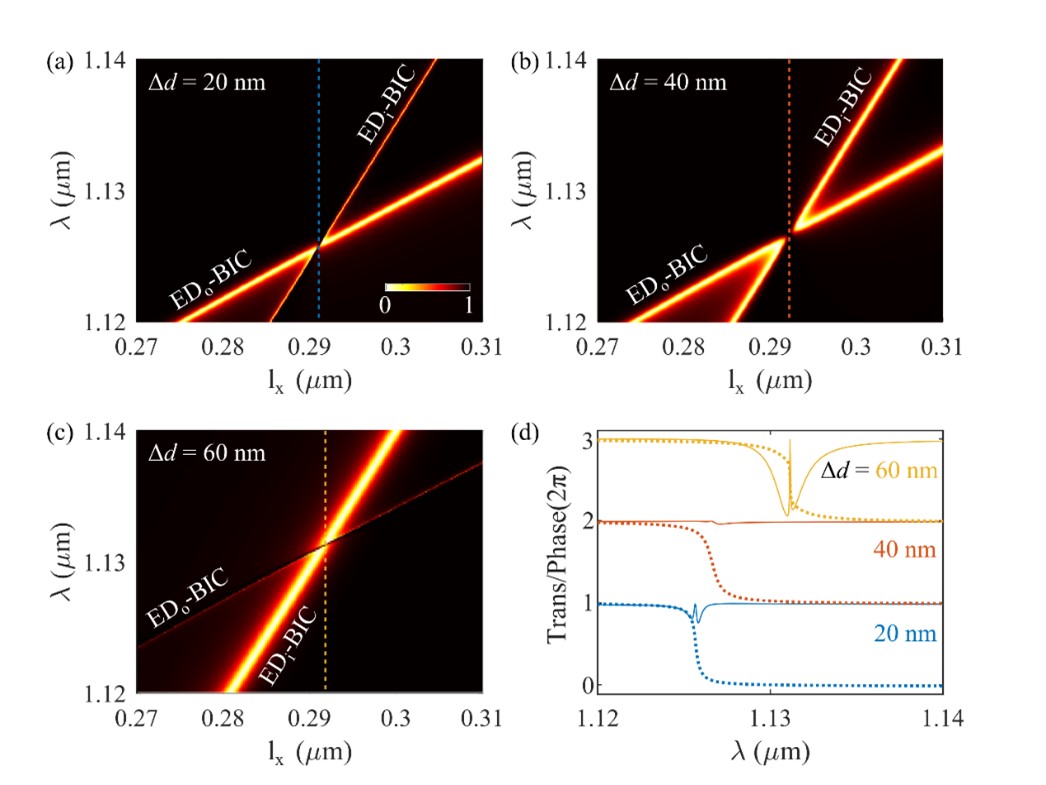
图3 在不同程度的RS扰动下，EDi-QBIC和EDo-QBIC共振交叉特性的变化规律以及在交叉区域的光谱特性。

其次作者研究了两个非正交的MD-QBIC和EDo-QBICBIC模式的耦合行为，模式反交叉现象表明BIC模式的相互作用进入了强耦合的状态，在反交叉区域，两个模式的相干相消作用会出现一种新的Friedrich–Wintgen BIC模式。通过多极子展开理论分析，清晰的揭示了耦合过程中单元结构中的电偶极子模式和磁偶极子模式的杂化行为，如图4所示。

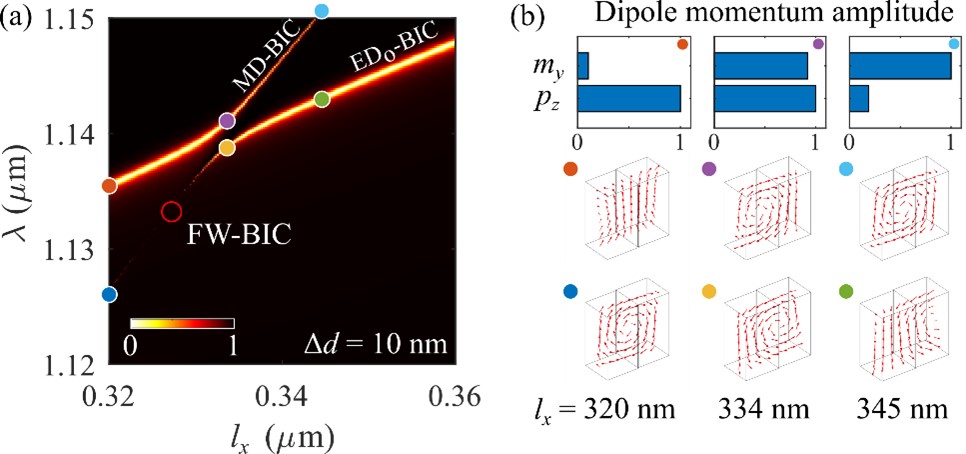
图4 MD-QBIC和EDo-QBIC耦合过程的共振反交叉特性以及QBIC模式的模场特性

本文结果可为未来基于硫系超构表面共振增强的光吸收、非线性效应、纳米激光等相关研究提供重要参考。